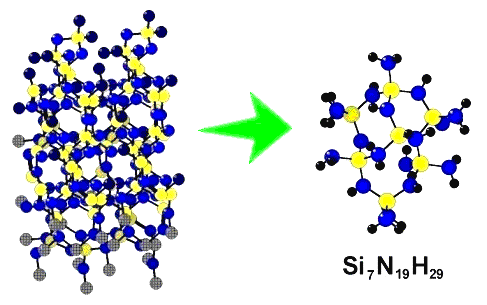
Interaction between adsorbate molecules and the surface of adsorbent is usually studied in the framework of the so-called cluster approximation. The cluster is just a fragment isolated from a three-dimensional ordered array of atoms constituting the crystal lattice. Broken bonds are saturated by appropriate simple residues, like hydrogen or hydroxy groups, the choice of which may alter from system to system. An example is shown in the next figure.
|
|
Figure 1. A molecular model of the surface of silicon nitride. The cluster pictured to the right has been isolated from the crystal lattice of β-Si3N4 shown to the left, broken bonds saturated by hydrogen atoms, and the resulting molecular structure optimized ab initio using the minimal Slater basis set STO-3G. |
Depending on complexity of the problem in question, theoretical computations of adsorbate structure can be performed using a variety of methods, ranging from atom-atom potential approximation to ab initio molecular orbital or density functional calculations.
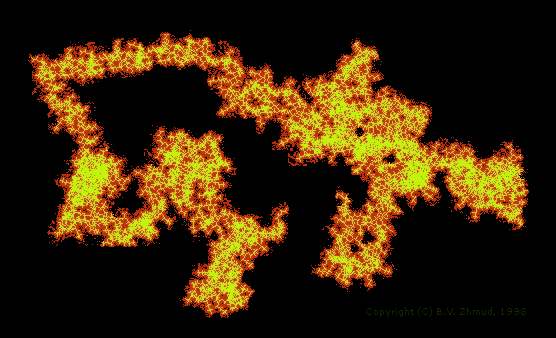
The conformational analysis of large polyfunctional molecules, such as surfactants and biopolymers, in soluted or adsorbed states is a very challinging task for the theoretical chemist. Such an analysis necessitates evaluation of hydration energies characterizing solute-water interaction. A knowledge of the hydration free energies makes it possible to better understand the driving forces of conformational transformations in solution, micelle formation, phase separation, etc. Since the problem of intermolecular interactions is an extremely complex one - it's sufficient to say that the problem of dispersion interactions cannot be adequately addressed without taking into account the electron correlation - the rigorous statistical and quantum mechanic methods appear to be of little use here. That's why the simpler molecular mechanic approach remains a viable alternative to the use of more rigorous methods. Properly parametrized models can afford sufficiently accurate results with minimum computational resources. An illustrative example is brought below:
|
|
Figure 2. The random coil configuration of ethyl(hydroxyethyl)cellulose polymer of molecular weight 103802. The solvent accessible surface area of this monster is about 894 nm2, yielding the hydration free energy of ca. -5587 kcal/mol. Calculations were carried out using the OMNISOL program [G.D. Hawkins, et al., J. Phys. Chem. 101(1997)7147] revisited and ported on an Intelx86 PC platform. |
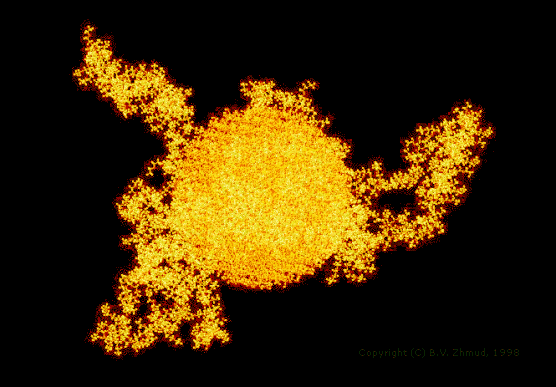
Not less important is the fact that you can see your systems in real size. The next illustration shows the same EHEC macromolecule adsorbed to the surface of a silica nanoparticle.
|
|
Figure 3. The configuration of the EHEC macromolecule (MW ~ 103802; 15302 atoms) adsorbed at the surface of a spherical silica particle having the radius of 33.5 Å and containing 11433 constituent atoms situated in the lattice of high cristobalite with terminal bonds saturated by adding 1026 hydrogen atoms to get an ideal hydroxylated surface. The visualization software: Hyperchem, Release 2 (Hypercube, Inc.) |